Ukuran Sudut ( Derajat dan Radian)

PENGUKURAN SUDUT

(Derajat dan Radian)

        Selamat datang kepada kawan kawan bang de, pada postingan kali ini kita akan memasuki materi baru yaitu tentang Trigonometri dengan Kompetensi Dasar : 3.6 Menjelaskan rasio trigonometri    (sinus, cosinus, tangen,cosecant,secan, dan cotangen) pada segitiga siku-siku. 4.6 Menyelesaikan masalah kontekstual yang bekaitan dengan rasio trigonometri (sinus, cosinus, tangen,cosecant,secan, dan cotangent) pada segitiga siku- siku. Pada pertemuan pertama kita akan membahas Pengukuran Sudut. Kawan kawan diharapkan mampu menyatakan hubungan radian ke derajat dan sebaliknya, menyelesaikan masalah yang berkaitan dengan hubungan radian ke derajat dan derajat ke radian.

1.

1. Sudut 

Sudut adalah suatu daerah yang dibentuk oleh dua buah ruas garis yang titik pangkalnya sama.

        Ruas garis AB dan AC disebut kaki sudut, ditulis AB dan AC dan titik A disebut titik sudut. Daerah yang dibatasi kaki sudut, daerah yang diarsir disebut daerah sudut. Besar daerah sudut cukup disebut besar sudut. Kedua gambar di atas, menunjukkan besar sudut yang sama walaupun panjang kaki-kaki sudutnya tidak sama panjang. Jadi dapat disimpulkan bahwa besar sudut tidak ditentukan oleh panjangnya kaki sudut.

2.  Ukuran Sudut 

Konsep dasar sudut

        Dalam kajian geometris sudut didefinisikan sebagai hasil rotasi dari sisi awal (initial side) ke sisi akhir (terminal side). Selain itu, arah putaran memiliki makna dalam sudut. Suatu sudut bertanda “positif” jika arah putarannya berlawanan dengan arah jarum jam dan bertanda “negatif” jika arah putarannya searah dengan jarum jam.

    Pada umumnya ada dua ukuran yang digunakan untuk menentukan besar suatu sudut yaitu derajat dan radian. Tanda “ ° ”  simbol dari derajat dan “rad” menyatakan simbol radian.

a.  Ukuran sudut dalam derajat

Besar suatu sudut dalam derajat dapat dijelaskan menggunakan konsep sudut sebagai jarak putar.

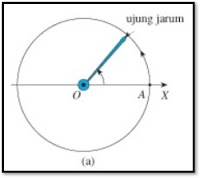
            Pada gambar (a) di perlihatkan sebuah jarum jam yang dapat berputar bebas terhadap titik pangkal jarum. Titik pangkal ini diberi nama titik O dan titik O terletak pada garis mendatar OX. Misalkan titik ujung jarum mula-mula berada pada titik A (A berada pada garis  ) sehingga sudut yang di bentuk jarum oleh jarum jam terhadap OX sama dengan nol derajat (0°). Kemudian jarum jam diputar berlawanan arah dengan arah gerak jarum jam biasa sehingga diperoleh hasil seperti di tunjukan pada gambar (a). Sudut antara jarum dengan garis OX merupakan jarak putar dan sudut tersebutakan semakin besar jika jarak putarannya diperbesar.

        Gerak  jarum jam dalam deskripsi di atas dapat dituliskan oleh gerak dari jari- jari lingkaran seperti di perlihatkan pada gambar dibawah ini 

        Sehingga ukuran besar sudut ditentukan oleh jarak putar jari – jari lingkaran terhadap garis OX. Sekarang jika jarum digerakkan sehingga ujungnya yang semula di A berpindah ke B,kemudian ke C,dan kembali lagi ke A, maka dikatakan jarum ini bergerak dalam satu putaran. Panjang lintasan yang dilalui oleh titik ujung jarum sama dengan keliling lingkaran dan besar sudut yang disapu oleh jarum sama dengan 360°. 

Berdasarkan deskripsi di atas, ukuran sudut dalam derajat dapat di definiskan sebagai berikut :

b. Ukuran sudut dalam radian 

    Gambar menunjukkan tiga lingkaran yang konsentris (sepusat) di titik O dan dapat disusun perbandingan sebagai berikut.

                                    Perhatikan gambar di bawah ini.

Gambar (i) menunjukkan besar sudut 1 radian, yaitu sudut pusat juring di hadapan busur yang panjangnya r, maka besar sudut ∠AOB = 1 rad

Gambar (ii) menunjukkan panjang busur ABC = 2r, maka besar sudut ∠AOC = 2 rad

Gambar (iii) menunjukkan panjang busur ABCD = 3r, maka besar sudut ∠AOD = 3 rad

3. Mengubah ukuran sudut dari derajat ke radian dan sebaliknya 

    

        Kita telah mengetahui bahwa panjang busur =r pada keliling lingkaran membentuk sudut 1 radian di pusat lingkaran. Keliling lingkaran =2πr ,berarti keliling lingkaran (2πr) membentuk sudut 2π radian di pusat lingkaran, sementara itu, sudut pusat lingkaran = 360°.

 

Ayo tentukan hubungan antara radian dan derajat !