
Kompetensi
Dasar :
3.1 Menginterpretasi persamaan dan
pertidaksamaan nilai mutlak dari bentuk linier satu variabel dengan persamaan
dan pertidaksamaan linier Aljabar lainnya
4.1 Menyelesaian masalah yang berkaitan
dengan persamaan dan pertidaksamaan nilai mutlak dari bentuk linier satu variable
Indikator
Pencapaian kompetensi
3.1.4 Menjelaskan pertidaksamaan nilai mutlak
satu variabel dari bentuk linier satu variabel ke bentuk pertidaksamaan linier
Aljabar lainnya (dengan definisi)
4.1.4 Menyelesaikan masalah yang berkaitan
dengan penyelesaian pertidaksamaan nilai mutlak
linier satu variabel
Tujuan
Pembelajaran
v Siswa dapat menentukan penyelesaian pertidaksamaan
nilai mutlak linier satu variabel dengan benar,jika diberikan pertidaksamaan
nilai mutlak linier satu variable
v Siswa dapat menyelesaikan masalah yang
berkaitan dengan pertidaksamaan nilai mutlak linier satu variabel dengan benar,
jika diberikan masalah kontekstual
Sebelum kawan
kawan mempelajari Pertidaksamaan nilai mutlak, sebaiknya kawan kawan mengingat Kembali
atau membaca lagi materi berikut ini agar memudahkan untuk memahami
pertidaksamaan nilai mutlak. Baiklah semoga postingan ini bisa membantu kawan kawan semua untuk belajar dari rumah.
Selamat belajar

Ø Pertidaksamaan linear adalah pertidaksamaan yang variabelnya paling tinggi berderajat satu
Ø Pertidaksamaan adalah kalimat terbuka yang dihubungkan oleh notasi ketidaksamaan

Ø
Bentuk-bentuk pertidaksamaan
ax + b > 0, ax + b <
0, ax + b ≥ 0 , ax + b ≤ 0
Ø Contoh dari bentuk pertidaksamaan linier satu variabel antara lain :
Ø Konsep nilai mutlak
Nilai mutlak dari suatu bilangan adalah jaraknya terhadap nol pada suatu
garis bilangan. Nilai mutlak suatu bilangan bernilai lebih dari atau sama
dengan nol.
Definisi 1.1




2. Selisih
antara panjang dan lebar suatu persegi panjang kurang dari 6 cm. Jika keliling
persegi panjang adalah 32 cm, maka tentukan batas nilai lebar persegi panjang
tersebut.
Penyelesaian
Diketahui : misalkan panjang persegi panjang adalah p dan lebar persegi panjang adalah
l.
keliling persegi
panjang = 2(p + l)= 32 cm, p
+ l < 6
Ditanya : batas nilai lebar persegi panjang
Selanjutnya , karena selisih antara panjang dan lebar
persegi kurang dari 6 cm, maka
di part 2 kita akan lebih banyak membahas soal pertidaksamaan dengan bentuk
jadikan refrensi belajar matematika mu..

.png)

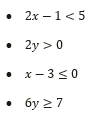




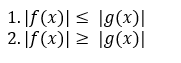





0 Comments